The butterfly effect is a deterministic nonlinear system’s sensitive dependence on initial conditions, in which a small change in one state can result in large differences in a later state.
The term is closely associated with Edward Norton Lorenz, a mathematician, and meteorologist. The butterfly effect, he explained, is based on the metaphorical example of tornado details (exact time of formation, exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull to cause a storm, but by 1972, he had been persuaded to use a butterfly and a tornado to make it more poetic.
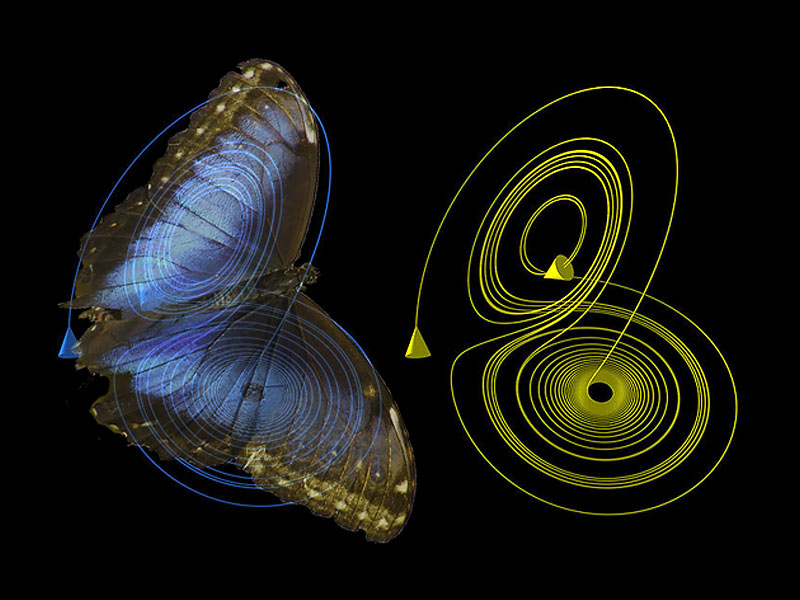
Lorenz discovered the effect after observing runs of his weather model with initial condition data that were rounded in an insignificant way. He observed that the results of runs with unrounded initial condition data would not be reproduced by the weather model. A very minor change in the starting conditions had resulted in a significantly different outcome.
Henri Poincaré, a French mathematician and engineer, was the first to recognize that small causes can have large effects on weather. Norbert Wiener, an American mathematician, and philosopher, also contributed to this theory. Lorenz’s work quantitatively established the concept of instability in the Earth’s atmosphere and linked it to the properties of large classes of dynamic systems undergoing nonlinear dynamics.

Outside of the context of weather science, the butterfly effect concept has since been used as a broad term for any situation in which a small change is thought to be the cause of larger consequences.
Johann Gottlieb Fichte writes in The Vocation of Man (1800) that “you could not remove a single grain of sand from its place without thereby… changing something throughout all parts of the immeasurable whole.”

Numerous forms of literature have described chaos theory and the sensitive dependence on initial conditions. This is demonstrated by Poincaré’s case of the three-body problem in 1890. He later proposed that such phenomena, for example, could be common in meteorology.
Jacques Hadamard discovered a general divergence of trajectories in negative curvature spaces in 1898. In 1908, Pierre Duhem discussed the broader implications of this.
The idea that the death of one butterfly could have far-reaching ramifications on subsequent historical events first appeared in Ray Bradbury’s short story “A Sound of Thunder” in 1952. The movie “A Sound of Thunder” dealt with the possibility of time travel.

Lorenz was using a numerical computer model in 1961 to redo a weather prediction from the middle of the previous run. Instead of entering the full precision 0.506127 value, he used the initial condition 0.506 from the printout. As a result, the weather scenario changed drastically.
Following suggestions from colleagues, Lorenz began using the more poetic butterfly in later speeches and papers. When Lorenz couldn’t think of a title for a talk he was giving at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees came up with Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? according to Lorenz.

Although the image of a butterfly flapping its wings has remained consistent throughout this concept, the butterfly’s location, the consequences, and the location of the consequences have all changed.
As a result, the weather scenario changed drastically.
Following suggestions from colleagues, Lorenz began using the more poetic butterfly in later speeches and papers.
When Lorenz couldn’t think of a title for a talk he was giving at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees came up with Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas? according to Lorenz.
Although the image of a butterfly flapping its wings has remained consistent throughout this concept, the butterfly’s location, the consequences, and the location of the consequences have all changed.

The flapping wing represents a minor change in the system’s initial state, which leads to large-scale changes in events (compare: domino effect). The system’s trajectory might have been vastly different if the butterfly hadn’t flapped its wings, but it’s also possible that the set of conditions without the butterfly flapping its wings is the set that leads to a tornado.
Also read: What is the Science Behind the Cryogenic Engines
Because initial conditions for a system like the weather can never be known with 100% accuracy, the butterfly effect presents an obvious challenge to prediction. The development of ensemble forecasting, in which a number of forecasts are made from perturbed initial conditions, was motivated by this problem.
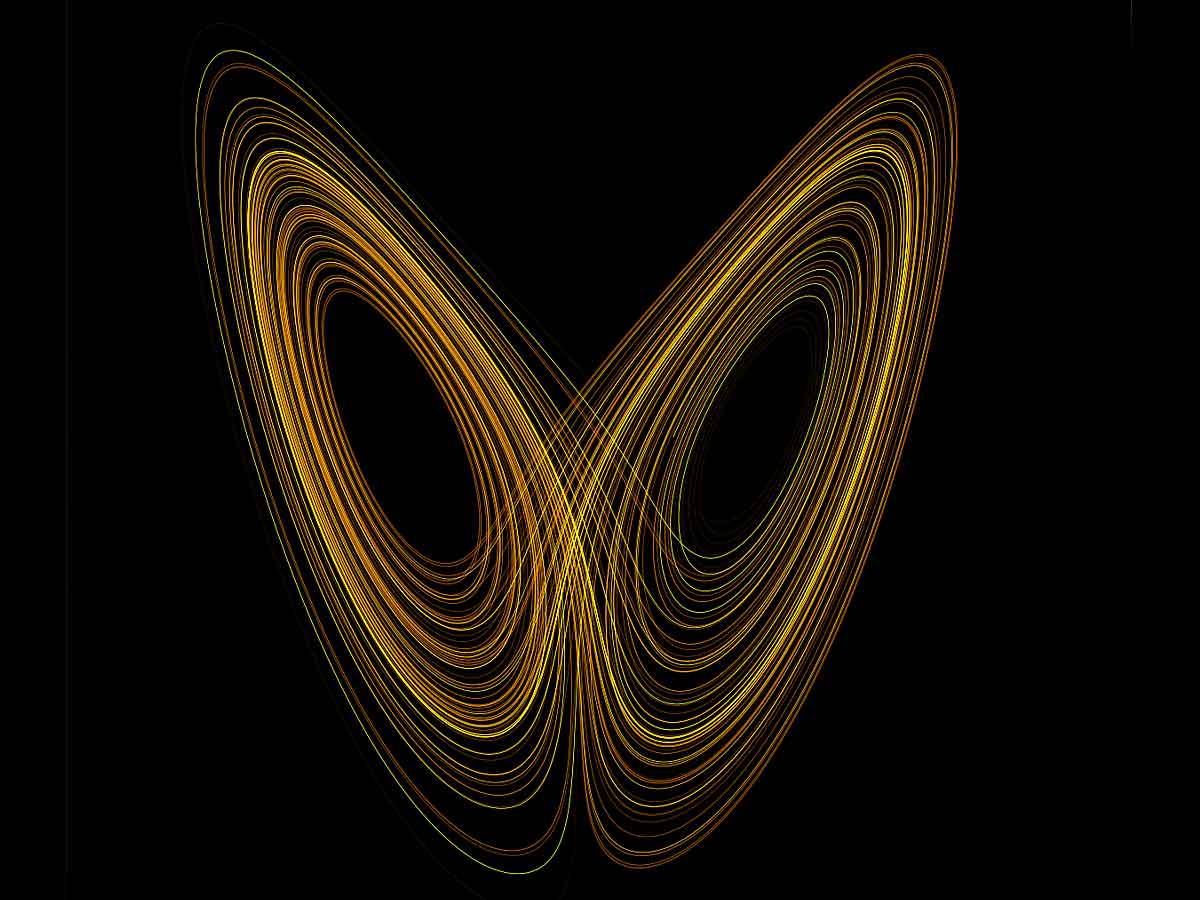
Since then, some scientists have argued that the weather system is less sensitive to initial conditions than previously thought. Model error, according to David Orrell, is the major contributor to weather forecast error, with sensitivity to initial conditions playing a minor role. Stephen Wolfram also points out that the Lorenz equations are oversimplified and lack terms that represent viscous effects, which he believes would dampen small perturbations.
While the “butterfly effect” is frequently associated with sensitive dependence on initial conditions such as those described by Lorenz in his 1963 paper (and previously observed by Poincaré), the butterfly metaphor was first applied to work he published in 1969 that took the idea a step further.

Lorenz proposed a mathematical model for how small atmospheric motions can affect larger systems. He discovered that the systems in that model could only be predicted up to a certain point in the future and that reducing the error in the initial conditions did not improve predictability beyond that point (as long as the error is not zero).
This showed that in terms of predictability, a deterministic system could be “observationally indistinguishable” from a non-deterministic one. Recent re-examinations of this paper suggest that it posed a significant challenge to the idea of determinism in our universe, comparable to quantum physics’ challenges.




























